Nieuwste buitenlandse casino’s
De nieuwste buitenlandse casino’s, zoals Monixbet, LocoWin, Loki Casino, en Manga Casino, zijn enkele casino’s die pas sinds enkele jaren bestaan. Gokken bij nieuwe buitenlandse casinos biedt ook enkele voordelen. Deze casino’s hebben vaak meer en hogere welkomstbonussen om nieuwe spelers aan te trekken. Daarnaast hebben ze vaak de nieuwste spellen in hun spelaanbod. Dat is leuk als je graag nieuwe games uitprobeert. Plus je krijgt ook vaak free spins om nieuwe games uit te proberen!

Hieronder vind je een overzicht van vijf van de nieuwste games die in 2025 zijn uitgebracht, en in welk buitenlandse casino je ze kan spelen:
| Game | Spelontwikkelaar | RTP % | Thema | Waar speel je? |
|---|---|---|---|---|
| Treasure of the Lost City | NetEnt | 96.5% | Avontuur | Boomerang.bet |
| Dragon’s Fire: Inferno | Red Tiger Gaming | 95.7% | Fantasie | LocoWin |
| Mystic Forest | Microgaming | 96.2% | Magie | Loki Casino |
| Galactic Gold Rush | Yggdrasil | 96.8% | Sciencefiction | Manga Casino |
| Viking’s Voyage | Play’n GO | 96.1% | Vikingen | Monxibet |
Lees hieronder verder om onze top 10 beste online buitenlandse casino’s te ontdekken, het beste bonus aanbod, betaalmethoden, en nog veel meer.
Top 10 betrouwbare online casino’s in het buitenland
We hebben onze top 10 buitenlandse casino’s voor Nederlandse spelers belangrijkste info op een rij gezet. Zo kan je in 1 oogopslag zien welk buitenlands casino het beste is voor jou.
| Casino | Opgericht | Games | Opnametijd | RTP | Inzetlimiet | Opname limiet |
|---|---|---|---|---|---|---|
| Monixbet | 2024 | 6000+ | 1-3 werkdagen | 98% | €5 | €10.000 per transactie |
| CrazePlay Casino | 2019 | 3500+ | 1-3 werkdagen | 96% | €5 | €10.000 per maand |
| Locowin Casino | 2022 | 3500+ | 1-2 werkdagen | 95% | €5 | €50.000 per maand |
| Loki Casino | 2023 | 9500+ | 5-7 werkdagen | 96% | €5 | €5.000 per transactie |
| Manga Casino | 2023 | 3000+ | 1-3 werkdagen | 98% | €5 | €1.000 per dag |
| Seven Casino | 2023 | 2400+ | 3 werkdagen | 96% | €2 | €10.000 per transactie |
| Palm Casino | 2023 | 2000+ | 3 werkdagen | 96% | €2 | €1.000 per dag |
| Qbet | 2022 | 2000+ | 1-3 werkdagen | 98% | €6 | €10.000 per transactie |
| Rakoo Casino | 2023 | 6000+ | 3 werkdagen | 96% | €5 | €10.000 per transactie |
| Rant Casino | 2020 | 4000+ | 3-5 werkdagen | 96% | €5 | €10.000 per transactie |

Hoe kies je betrouwbare buitenlandse casinos online?
Het kiezen van betrouwbare online casino’s in het buitenland kan uitdagend zijn. Hier zijn enkele tips om je te helpen:
Geldige licentie
Een gokvergunning garandeert dat het buitenlands casino online waar je speelt betrouwbaar en veilig is. Wanneer je dus een online casino in het buitenland kiest, kijk dan altijd goed naar de licentie. Deze staat meestal in de footer van de buitenlandse casino sites en je kan deze ook terugvinden op de website van de licentie uitgever. Zo weet je 100% zeker dat het casino een gokvergunning heeft, en voldoet aan de strenge veiligheidseisen die daarbij komen kijken.
Wanneer je voor echt geld gokt, is het zeker een belangrijk aspect om mee te nemen wanneer je een buitenlands casino kiest. Onze top 10 betrouwbare buitenlandse casinos hebben allemaal een vergunning en zijn zodoende veilige opties om bij te gokken.
| Buitenlandse licentie | Belangrijkste kenmerk |
|---|---|
| MGA (Malta Gaming Authority) | Prestigieuze en gerespecteerde licentie, biedt een hoog niveau van spelersbescherming. |
| Curaçao eGaming | Toegankelijke en eenvoudig te verkrijgen licentie, populair bij buitenlandse casino’s. |
| KGC (Kahnawake Gaming Commission) | Licentie gericht op Canadese spelers, biedt eerlijk spel. |
| UKGC (United Kingdom Gambling Commission) | Strenge eisen aan casino’s, maar biedt een hoog niveau van spelersbescherming. |
| Gibraltar Gambling Commissioner | Betrouwbare en gerespecteerde licentie. |
| Isle of Man Gambling Supervision Commission | Licentie gericht op de Europese markt, biedt eerlijk en transparant spel. |
| Estonian Gambling Authority | Nieuwe licentie, wint snel aan populariteit, biedt gunstige voorwaarden voor casino’s. |
| Jersey Gambling Commission | Strenge eisen aan casino’s, maar biedt een hoog niveau van spelersbescherming. |
Games van bekende spelontwikkelaars
Het spelaanbod van een online buitenlands casino kan je tevens de nodige informatie geven over de betrouwbaarheid en veiligheid van een online casino in het buitenland. Wanneer het casino games aanbiedt van gerenommeerde spelontwikkelaars zoals NetEnt, Microgaming en Playtech onder meer, dan kan je er vrijwel zeker van zijn dat je bij een betrouwbaar casino speelt. Deze ontwikkelaars waarborgen de Return to Player (RTP) en de Random Number Generator (RNG), dus de uitkomsten van de spellen zijn eerlijk en willekeurig.
Kortom, wanneer je in het spelaanbod van een buitenlands casino kijkt en er staan louter games tussen van bekende en populaire spelontwikkelaars, dan kan je ervan verzekerd zijn dat het casino veilig is en de gokspellen eerlijk zullen zijn.
| Ontwikkelaar | Meest populaire spel | RTP |
|---|---|---|
| NetEnt | Starburst | 96,09% |
| Play’n GO | Book of Dead | 96,21% |
| Games Global | Gonzo’s Quest | 95,97% |
| Pragmatic Play | Sweet Bonanza | 96,51% |
| Spinomenal | Book of Rebirth | 96,79% |
| Red Tiger | Gonzo’s Quest Megaways | 96,21% |
| Playtech | Age of the Gods | 95,64% |
| Novomatic | Book of Ra Deluxe | 95,10% |
| Quickspin | Vikings Go Berzerk | 96,58% |
| BGaming | Fruit Nova | 96,44% |
Veilige betaalmethoden
Een andere manier om te achterhalen of een casino betrouwbaar is, is door te kijken naar de betaalopties die ze bieden. Wanneer casino’s samenwerken met bekende betaalmethoden zoals iDEAL, creditcards zoals VISA en Mastercard, Paypal, Skrill enzovoort, dan weet je dat je transacties veilig zullen verlopen.
Het feit dat de meeste online buitenlandse casino’s online veel betaalopties aanbieden, geeft jou als speler ook meer flexibiliteit. Het heeft natuurlijk geen zin een account aan te maken wanneer je vervolgens geen geld kan storten om ook daadwerkelijk te gokken. Dus wanneer jij een casino kiest, moet je voorafgaand altijd eerst de betaalmethoden checken.
| Betaalmethoden | Storting/uitbetaling | Betaalsnelheid | Beschikbaarheid |
|---|---|---|---|
| Creditcards | ✔️/✔️ | tot 24 uur | overal |
| iDEAL | ✔️/✔️ | tot 1 uur | zelden |
| Trustly | ✔️/✔️ | enkele minuten | vaak |
| PayPal | ✔️/✔️ | enkele minuten | vaak |
| Skrill, Neteller | ✔️/✔️ | tot 1 uur | vaak |
| PaysafeCard | ✔️/❌ | enkele minuten | zelden |
| Bank Transfer | ✔️/✔️ | tot 5 dagen | overal |
| Crypto | ✔️/✔️ | enkele minuten | vaak |
Goede klantenservice
Een goede klantenservice is ontzettend belangrijk wanneer je een buitenlands casino online kiest. Je wilt immers dat als er problemen zijn, je direct contact kan opnemen. Voor ons betekent een betrouwbare klantenservice eentje die 24/7 beschikbaar is en via meerdere kanalen communicatie aanbiedt. Zoals live chat, e-mail en telefoon. Een snelle reactie is evenmin van belang. Dit geeft je niet alleen gemoedsrust, maar verzekert je er ook van dat je altijd hulp kunt krijgen wanneer dat nodig is.
| Methode | Beschikbaarheid | Reactiesnelheid |
|---|---|---|
| ☎️ Telefoon | overal | 1-3 minuten |
| overal | Binnen 24 uur | |
| 💬 Live chat | overal | 1-3 minuten |
| 📃Sociale Media | zelden | Binnen 24 uur |
Positieve reviews van spelers
Een andere tip die we je kunnen meegeven is altijd de beoordelingen van andere spelers te lezen, om een idee te krijgen van hun ervaring met het online casino buitenland. Zoek naar reviews op betrouwbare review websites en let op als je terugkerende klachten ziet. Reviews van spelers zijn een goede aanduiding dat een online casino betrouwbaar en klantgericht is.
Betaalmethoden buitenlandse casino’s
Om in het casino online in het buitenland te spelen moet je wel nagaan of de betaalmethoden die ze bieden aansluiten bij jouw wensen. Gelukkig bieden meeste buitenlandse casino’s veel betaalopties aan want ze willen zo toegankelijk mogelijk zijn. Als je wilt checken welke betaalmethoden ze aanbieden, neem dan een kijkje op de footer van de website. Daar staan ze meestal allemaal middels een logo weergegeven. Een andere optie is de FAQ te bekijken. Wij zetten voor het gemak de populairste betaalmethoden in buitenlandse casino’s hieronder voor je uiteen.
iDEAL
Creditcard
E-wallets
Crypto
Maak een account bij het beste buitenlandse online casino
Als je al deze dingen hebt gecheckt, en je bent klaar om te spelen, dan maak je simpelweg een account bij jouw buitenlands casino van keuze.
Je kan bij buitenlandse casino’s sneller en makkelijker een account aanmaken dan een Nederlands casino. In tegenstelling tot het Nederlandse casino, hoef je namelijk bij online buitenlandse casinos geen identiteitsbewijs of paspoort te uploaden. Je hebt enkel een e-mailadres of een telefoonnummer nodig om een account aan te maken.
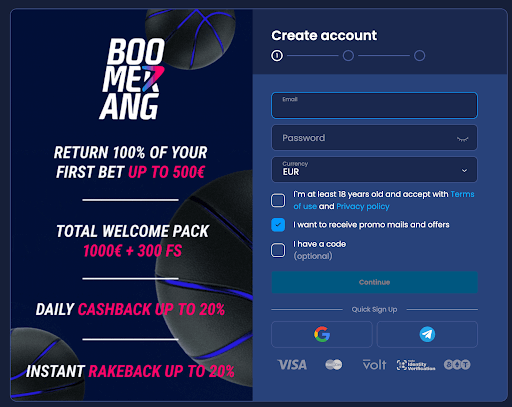
Volg deze 5 stappen om een account aan te maken bij Boomerang.bet. Als je liever een account aanmaakt bij een ander buitenlands casino dan zijn de stappen vrijwel hetzelfde.
Stap 1: Meld je aan
Ga naar onze nummer #1 buitenlands casino Boomerang.bet en klik op de knop “Sign Up” rechtsboven op de homepage. Je kunt je e-mailadres invullen en een wachtwoord kiezen, of snel een account aanmaken door je Google- of Telegram-informatie te gebruiken.
Stap 2: Bevestig je e-mailadres
Na het invullen van je gegevens en het kiezen van een wachtwoord, ontvang je een bevestigingsmail. Klik op de link in deze e-mail om je e-mailadres te bevestigen en je account te activeren.
Stap 3: Maak een eerste storting
Zodra je een wachtwoord hebt gekozen, verschijnt er direct een pop-up voor je eerste storting. Kies het bedrag dat je wilt storten en je betaalmethode.

Stap 4: Claim de welkomstbonus
Maak je eerste storting en claim direct het welkomstaanbod van Boomerang.bet. Je kunt tot €500 aan bonussen en 200 gratis spins ontvangen. Volg de instructies op het scherm om je bonus te claimen.
Stap 5: Begin met Spelen
Na je eerste storting en het claimen van je bonus, ben je klaar om te beginnen met spelen. Kies je favoriete spel, of probeer een nieuwe. Of neem een kijkje welk sportevenement er is om op te wedden en plaats een wedje op jouw favo sport!

Online casino spelen in het buitenland – 5 tips
Omdat het belangrijk is dat je niet alleen het beste buitenlandse casino voor Nederlands kiest, maar ook dat je het meeste voordeel haalt wanneer je begint met spelen, geven wij je enkele nuttige tips! Op deze manier kan je veiliger en slimmer spelen, en optimaal profiteren van de beschikbare bonussen en promoties.
- Maak gebruik van bonussen: Meld je aan bij meerdere casino’s om van verschillende bonus aanbiedingen te profiteren. Kies het perfecte moment uit wanneer de welkomstbonus hoog is en meld je dan aan als nieuwe speler.
- Controleer de licentie: Speel alleen bij buitenlandse casino’s met een geldige en erkende goklicentie, bijvoorbeeld van de MGA of eGaming Curaçao, dit zijn bekende en veilige licenties.
- Let op je bankroll: Stel een budget in en houd je eraan om verantwoord te spelen. Zo voorkom je dat je meer uitgeeft dan je je kunt veroorloven.
- Neem regelmatig pauzes: Voorkom vermoeidheid en blijf scherp tijdens het spelen door regelmatig pauzes te nemen. Dit helpt je om betere beslissingen te nemen en je speeltijd te verlengen.
- Lees de voorwaarden: Begrijp de inzetvereisten en voorwaarden van bonussen voordat je ze accepteert, zodat je precies weet wat er van je verwacht wordt en je onaangename verrassingen vermijdt.
Welk online casino buitenland kies jij?
Het kiezen van een buitenlands online casino kan uitdagend zijn, maar met de juiste informatie kun je een weloverwogen beslissing nemen. In dit artikel hebben we besproken wat de belangrijkste factoren zijn wanneer je buitelandse casino sites kiest om te gokken. Buitenlandse casinos die betrouwbaar zijn hebben altijd geldige licenties, een breed spelaanbod en uitstekende klantenservice zijn betrouwbare opties.
Ons favoriet all-round online casino in het buitenland is Monixbet. Het biedt alles wat je nodig hebt voor een veilige en lucratieve gokervaring, inclusief snelle opnametijden, diverse betaalmethoden, en een geweldig welkomstaanbod.

Buitenlandse casino FAQ
Buitenlandse online casino’s zijn goksites zonder Nederlandse vergunning. In een casino online in het buitenland zijn er minder beperkingen. Plus, je vindt in de meeste buitenlandse casino’s een groter spelaanbod en betere bonussen, die je in Nederland niet kan vinden.
Het beste buitenlandse online casino is Boomerang.bet. Wij hebben dit bepaald vanwege het uitgebreide spelaanbod dat het casino biedt, de aantrekkelijke bonussen, en betrouwbare klantenservice.
Ja, de meeste buitenlandse casino’s, waaronder ook Boomerang.bet, hebben mobiele apps van hun platform. Zo kan je ook onderweg een wedje wagen.
Alle buitenlandse casino’s in onze top 10 lijst zijn betrouwbare partijen om bij te gokken. Buitenlandse casinos die betrouwbaar zijn hebben altijd een geldige licentie, een groot aanbod aan spellen en veilige betaalmethoden